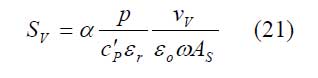Wie funktioniert ein pyroelektrischer Infrarotsensor?
Wie ist ein pyroelektrischer Infrarotsensor aufgebaut und wie kann seine Funktionsweise beschrieben werden? Was versteht man unter der spezifischen Detektivität und der Empfindlichkeit? Diese und weitere Fragen werden hier beantwortet.
Prinzipieller Aufbau und Funktionsweise eines pyroelektrischen Infrarotsensors
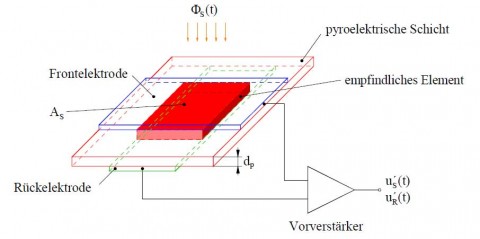
Bild 1 zeigt den prinzipiellen Aufbau eines pyroelektrischen Infrarotsensors. Wesentliche Bestandteile sind das empfindliche Element und der Vorverstärker, dessen wesentliche Elemente im Sensor integriert sind. Das empfindliche Element besteht aus einem dünnen, mit Elektroden versehenen pyroelektrischen Chip. Zur Verbesserung der Absorptionseigenschaften kann eine zusätzliche Schwarzschicht vorhanden sein.
Bild 1: Prinzipieller Aufbau eines pyroelektrischen Infrarotsensors
Trifft der Strahlungsfluss ΦS(t) auf die empfindliche Fläche AS, wird er vom empfindlichen Element mit dem Absorptionsgrad Α absorbiert. Dadurch entsteht im Pyroelektrikum eine Temperaturänderung ΔT(t), die zu einer Ladungsänderung ΔQ(t) auf den Elektroden führt. Diese Ladungsänderung wird mit Hilfe des Vorverstärkers in die Signalspannung uS´(t) umgewandelt.
Neben der Signalspannung ist am Ausgang des Vorverstärkers auch eine Rauschspannung uR´(t) vorhanden. Diese Rauschspannung hat ihre Ursache in den Rauschquellen sowohl des empfindlichen Elements als auch des Vorverstärkers. Sie bewirkt, dass kein beliebig geringer Strahlungsfluss vom Sensor nachgewiesen werden kann.
Sensorkenngrößen
Die wichtigsten Sensorkenngrößen sind die Empfindlichkeit SV, die rauschäquivalente Strahlungsleistung NEP und die spezifische Detektivität D*. Sie sind für sinusförmige Vorgänge im eingeschwungenen Zustand definiert und im allgemeinen von der Modulationsfrequenz f, der Wellenlänge λ und der Sensortemperatur T abhängig.
Empfindlichkeit eines IR Sensors
Die Empfindlichkeit SV ist der Quotient der Effektivwerte der sinusförmigen Signalspannung ũ‘S am Vorverstärkerausgang und des sinusförmig modulierten Strahlungsflusses 
, der auf die empfindliche Fläche AS trifft:
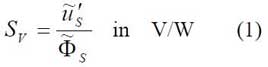
Die Empfindlichkeit als Quotient der Effektivwerte der sinusförmigen Signalspannung am Vorverstärkerausgang und des sinusförmig modulierten Strahlungsflusses
Rauschäquivalente Strahlungsleistung
Die rauschäquivalente Strahlungsleistung NEP ist eine das Signal/Rausch-Verhältnis charakterisierende Größe:
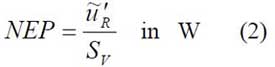
mit dem Effektivwert der Rauschspannung am Ausgang des Vorverstärkers ũ‘S.
Durch Kombination der Gleichungen (1) und (2) ist ersichtlich, dass die rauschäquivalente Strahlungsleistung dem Effektivwert des auftreffenenden Strahlungsflusses bei einem Signal/Rausch-Verhältnis ũ‘S / ũ‘R = 1 entspricht.
Spezifische Detektivität
Die spezifische Detektivität D* ist eine weitere, das Signal/Rausch-Verhältnis kennzeichnende Größe:
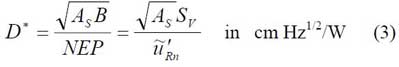
mit dem Effektivwert der auf eine Rauschbandbreite B = 1 Hz normierten Rauschspannung am Ausgang des Vorverstärkers
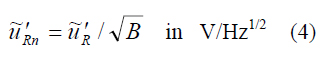
Die Definition der spezifischen Detektivität ermöglicht den einfachen Vergleich zwischen dem D*-Wert des realen Sensors und dem theoretischen D*-Limit. Dieses Limit ist nur von Naturkonstanten (Boltzmann-Konstante k, Stefan-Boltzmann-Konstante σ) und der Temperatur T abhängig:
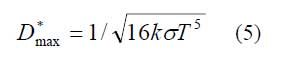
Für eine Temperatur von 300 K beträgt dieser Wert
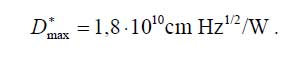
Pyroelektrisches Material
Das Pyroelektrikum nimmt als eigentliches Wandlerelement im pyroelektrischen Strahlungssensor eine zentrale Stellung ein. Von den 32 existierenden Kristallklassen besitzen Kristalle mit der Punktgruppensymmetrie 1, m, 2, mm2, 3, 3m, 4, 4mm, 6 und 6mm eine sogenannte spontane Polarisation, die das Auftreten des pyroelektrischen Effekts ermöglicht. Kristalle dieser Kristallklassen werden Pyroelektrika genannt. Technisch bedeutsam sind Pyroelektrika, bei denen die spontane Polarisation nur in einer einzigen Richtung im Kristall auftreten kann (einachsige Pyroelektrika). Dazu gehören die Kristallklassen 2, mm2, 3, 3m, 4, 4mm, 6 und 6mm. Die Richtung der spontanen Polarisation fällt mit der polaren Achse des Kristalls zusammen.
Für den Einsatz in pyroelektrischen Strahlungssensoren sind folgende Materialkenngrößen des Pyroelektrikums von Bedeutung:
p … pyroelektrischer Koeffizient
εr … Dielektrizitätszahl
tan δ … dielektrischer Verlust
cP‚ … volumenspezifische Wärmekapazität
Für hohe Werte von Empfindlichkeit SV und spezifischer Detektivität D* sind ein großer pyroelektrischer Koeffizient p und geringe Werte für die Dielektrizitätszahl εr, den dielektrischen Verlust tan δ und die volumenspezifische Wärmekapazität cP‚ erforderlich.
Seit vielen Jahren hat sich das Pyroelektrikum Lithiumtantalat (LiTaO3) beim Einsatz in pyroelektri-schen Sensoren bewährt. Es erfüllt nicht nur die eben genannten Forderungen an die Materialkenngrößen, sondern zeichnet sich auch durch eine ausgezeichnete Temperaturstabilität und sehr gute Reproduzierbarkeit der Sensoreigenschaften aus.
Typische Materialkenngrößen von LiTaO3 bei Raumtemperatur sind:
p = 1,8 · 10–8 C cn –2 K–1
εr = 43
tan δ = 0,001
cP‚ = 3,2 J cm–3 K–1
Ersatzschaltbilder des empfindlichen Elements und des Vorverstärkers
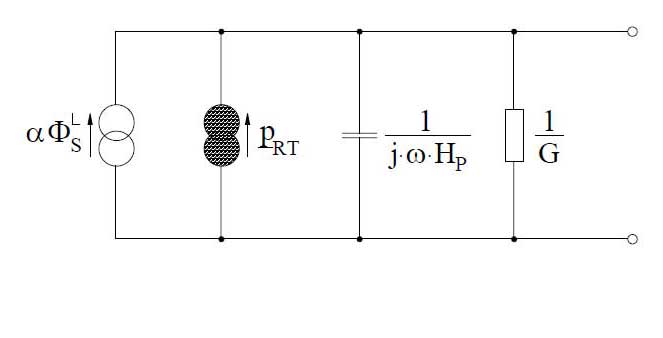
Die Absorption des Strahlungsflusses ΦS ruft im Pyroelektrikum eine Temperaturänderung ΔT hervor, die im allgemeinen vom Ort im Pyroelektrikum abhängt. Diese Ortsabhängigkeit kann oft in guter Näherung vernachlässigt werden, so dass das thermische Verhalten des empfindlichen Elements in diesen Fällen durch ein einfaches analoges elektrisches Ersatzschaltbild (Bild 2) mit der Wärmekapazität
und dem thermischen Leitwert G zwischen empfindlichen Element und seiner Umgebung dargestellt werden kann. Auf Grund des statistischen Charakters des Wärmeaustausches zwischen empfindlichem Element und Umgebung entsteht ein sogenanntes Temperaturrauschen. Deshalb ist im Bild 2 zusätzlich eine entsprechende Rauschquelle mit
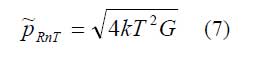
enthalten.
Die Temperaturänderung ΔT führt zu einem pyroelektrischen Strom, der bei Kurzschluss der Elektroden des empfindlichen Elementes fließt. Unter Berücksichtigung der Definition des pyroelektrischen Koeffizienten und der thermischen Verhältnisse nach Bild 2 ergibt sich dieser pyroelektrische Strom zu
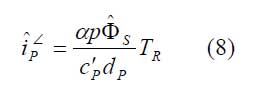
mit
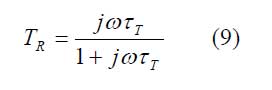
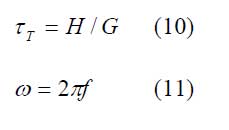
Die dimensionslose Funktion TR wird komplexe normierte Stromempfindlichkeit genannt. Für ein ideal thermisch isoliertes empfindliches Element (G = 0) erreicht die komplexe normierte Stromempfindlichkeit den Wert 1. Für praktisch interessante Modulationsfrequenzen f = 1 … 1000 Hz kann bei den meisten Sensorkonstruktionen näherungsweise auch mit diesem Wert 1 gearbeitet werden, weil die thermische Zeitkonstante τT entsprechende Werte erreicht. Wird die einfallende Strahlung nicht moduliert (f = 0), wird kein pyroelektrischer Strom erzeugt. Der pyroelektrische Sensor ist also nicht gleichlichtempfindlich. Er benötigt immer eine zeitliche Modulation des einfallenden Strahlungsflusses, z.B. durch Chopperung.
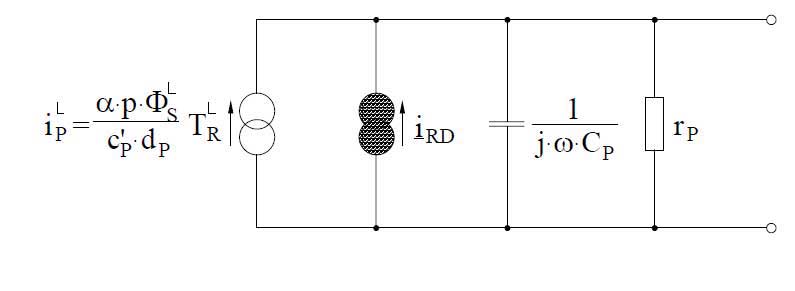
Bild 3 zeigt das elektrische Ersatzschalbild des empfindlichen Elements.
Eingangsgröße ist der pyroelektrische Strom nach Gleichung (8). Ersatzelemente sind die elektrische Kapazität
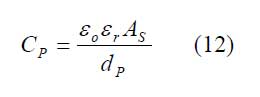
der frequenzabhängige Widerstand
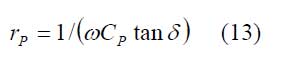
und die sogenannte tanδ
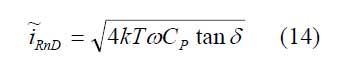
die das thermische Rauschen des Elementwiderstandes rP beschreibt.
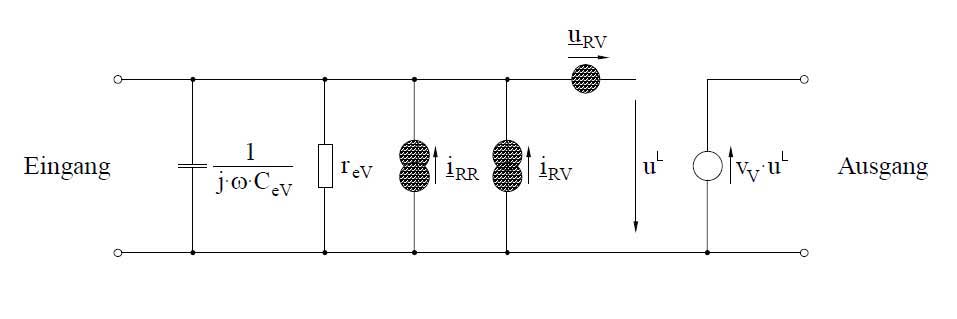
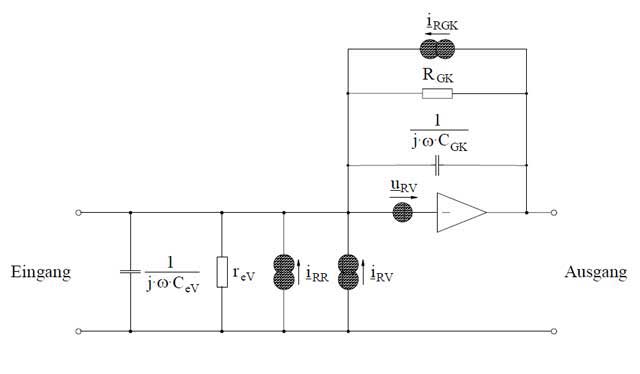
In den Bildern 4 und 5 sind die elektrischen Ersatzschaltbilder der zwei grundsätzlichen Vorverstärkerausführungen (Vorverstärker im Spannungs- oder Strombetrieb) dargestellt.
Ersatzelemente sind in beiden Fällen Eingangswiderstand reV und Eingangskapazität CeV sowie Strom- und Spannungsrauschen ĩRnV bzw. ũRnV des Vorverstärkers. Das thermische Rausches des Eingangswiderstandes beschreibt die Rauschquelle
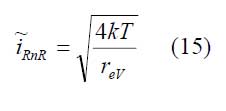
Beim Vorverstärker im Spannungsbetrieb wird zusätzlich die Verstärkung vV berücksichtigt. Der Vorverstärker im Strombetrieb enthält einen gegengekoppelten Operationsverstärker (Verstärkung → ∞) mit dem Gegenkopplungswiederstand RGK, dessen Kapazität CGK und dessen thermischem Rauschen
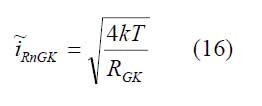
Empfindlichkeit
Aus der Definitionsgleichung (1) der Empfindlichkeit und den im vorhergehenden Abschnitt erläuterten Zusammenhängen folgt unmittelbar die für den Spannungsbetrieb des Vorverstärkers gültige Gleichung der Empfindlichkeit:
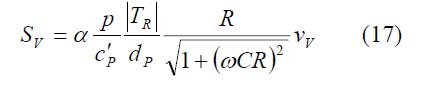
mit
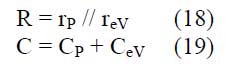
Die elektrische Zeitkonstante ergibt sich zu
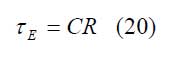
Oft gelten neben |TR| ≈ 1 auch (ωCR)2 >> 1 und CP >> CeV. Dann vereinfacht sich Gleichung (17) erheblich:
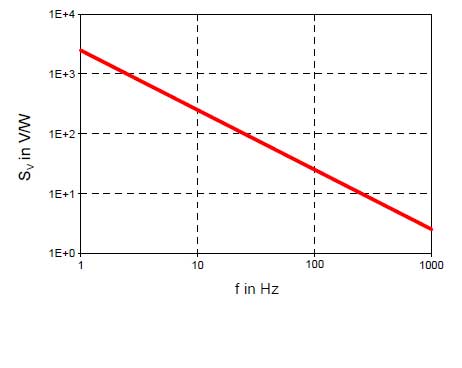
In diesem Fall ist die Empfindlichkeit indirekt proportional zur Modulationsfrequenz.
Für die Empfindlichkeit im Strombetrieb ergibt sich die Gleichung:
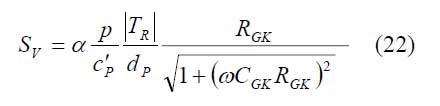
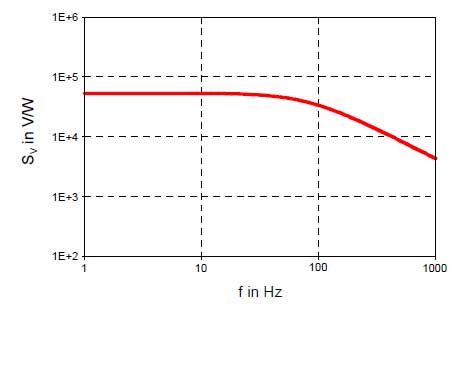
Wenn hier ebenfalls |TR| ≈ 1 und zusätzlich (ωCGKRGK)2 << 1 gelten, erhält man eine von der Modulationsfrequenz unabhängige Empfindlichkeit:
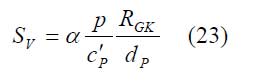
Für (ωCGKRGK)2 >> 1 gilt:
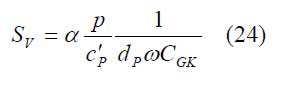
Normierte Rauschsspannung
Die im Abschnitt 4. angegebenen, nicht miteinander korrelierenden Rauschquellen rufen am Ausgang des Vorverstärkers Rauschspannungsanteile hervor. Die normierte Rauschspannung am Vorverstärkerausgang ergibt sich aus der quadratischen Addition der einzelnen Rauschspannungsanteile:
Vorverstärker im Spannungsbetrieb:
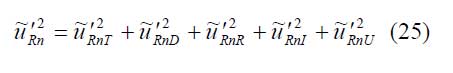
Vorverstärker im Strombetrieb:
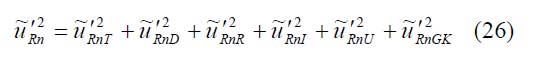
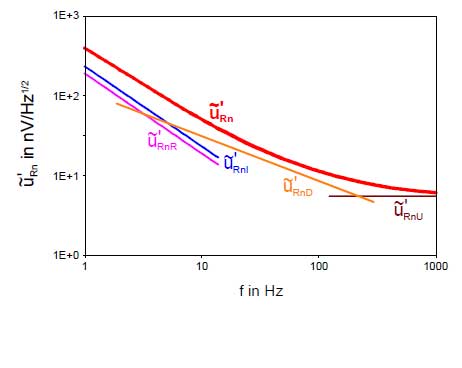
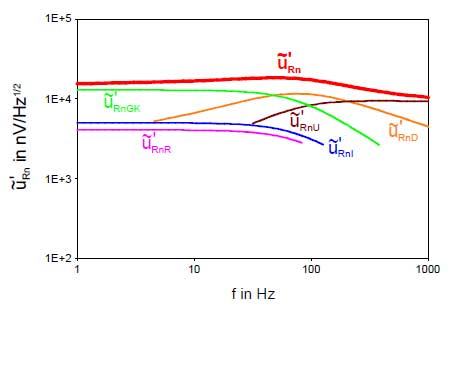
Die Gleichungen für die einzelnen Rauschspannungsanteile sind in Tabelle 1 zusammengestellt.
Spezifische Detektivität
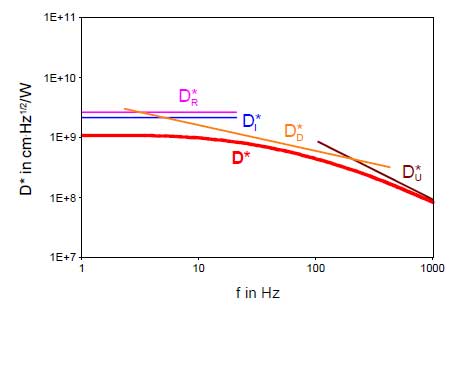
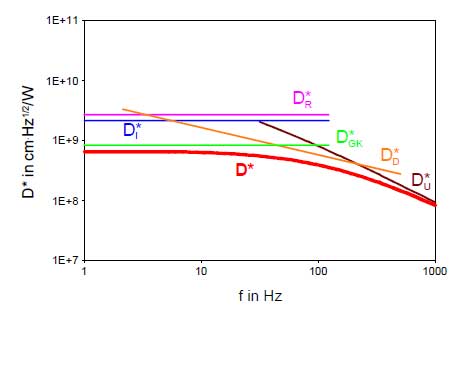
Aus der Definitionsgleichung (3) der spezifischen Detektivität sowie den Grundgleichungen der Empfindlichkeit (Abschnitt 5.) und normierten Rauschspannung (Abschnitt 6.) folgen die von den einzelnen Rauschspannungsanteilen hervorgerufenen Anteile der spezifischen Detektivität, dargestellt im Bild rechts.
Für die gesamte spezifische Detektivität gilt dann:
Vorverstärker im Spannungsbetrieb:
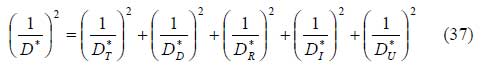
Vorverstärker im Strombetrieb:
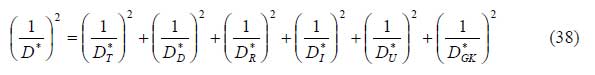
Die Gleichungen für die einzelnen Anteile der spezifischen Detektivität enthält Tabelle 2.
Beispiele
Für folgende Beispielsensoren werden in den Bildern 6 bis 11 die Frequenzgänge der Empfindlichkeit, der normierten Rauschspannung und der spezifischen Detektivität am Ausgang des Vorverstärkers dargestellt.
| Bildsensor | im Spannungsbetrieb | im Strombetrieb |
|---|---|---|
| Empfindliches Element | ||
| Pyroelektrikum | LiTaO3 | LiTaO3 |
| Empfindliche Fläche AS | 2 x 2 mm2 | 2 x 2 mm2 |
| Dicke dP | 5 µm | 5 µm |
| Absorptionsgrad α | 1 | 1 |
| Normierte Stromempfindlichkeit |TR| | 1 | – |
| Vorverstärker: | ||
| Eingangswiderstand reV | 1011 Ω | 1011 Ω |
| Eingangskapazität CeV | 2 pF | 2 pF |
| Verstärkung vV | 1 | – |
| Gegenkopplungswiderstand RGK | – | 1010 Ω |
| Gegenkopplungskapazität CGK | – | 0,2 pF |
| Stromrauschen ĩRnV (10 Hz) | 5 ⋅ 10–16 A/Hz1/2 | 5 ⋅ 10–16 A/Hz1/2 |
| Spannungsrauschen ũRnV (1 kHz) | 6 nV/Hz1/2 | 6 nV/Hz1/2 |
Bild 6: Frequenzgang der Empfindlichkeit im Spannungsbetrieb
Bild 7: Frequenzgang der Empfindlichkeit im Strombetrieb
Bild 8: Frequenzgang der normierten Rauschspannung im Spannungsbetrieb
Bild 9: Frequenzgang der normierten Rauschspannung im Strombetrieb
Bild 10: Frequenzgang der spezifischen Detektivität im Spannungsbetrieb
Bild 11: Frequenzgang der spezifischen Detektivität im Strombetrieb